Low-Rank Sparse Tensor Approximations for Large High-Resolution Videos

Abstract

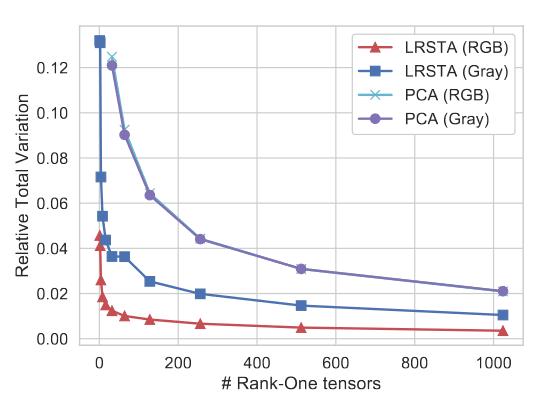
Tensor decomposition techniques are becoming increasingly important in processing videos with large sizes and dimensions. Under the framework of CANDECOMP/PARAFAC decomposition (CPD), this work studies low-rank sparse tensor approximations (LRSTAs) to higher-order tensors. Both theoretical and practical properties are evaluated for LRSTAs to represent large high-resolution videos. The evaluation brings three major contributions of this work. Firstly, the theoretical connection between CPD for high-order tensors and traditional singular value decomposition (SVD) for matrices are established, and the tensor rank for traditional SVD is defined. This provides a theoretical basis to compare tensor-based approach against matrix-based approach under the framework of tensor decompositions. Secondly, the non-orthogonality of CPD and its implications are revealed. The solution set of an LRSTA can only be used as a whole. Thirdly, a computationally efficient algorithm is developed. Its practical properties are also investigated in object detection and recognition in high-resolution videos. The results of the experiments showed that the proposed algorithm can handle large high-resolution videos very efficiently in terms of memory allocation. Results also revealed that commonly used total variations may not be a good evaluation metric for real world applications in computer vision. LRSTAs should be evaluated using the end goal of the applications, such as the accuracy of object detection and recognition.

Baijian Yang

Professor of Computer and Information Technology

My research interests include applied machine learning, big data and cybersecurity.